Semantic Entanglement: How Quantum Entanglement Illuminates the Inner Workings of Large Language Models

Getting your Trinity Audio player ready…

1. Introduction

Large Language Models (LLMs) are among the most powerful computational systems humanity has built. They can generate text that mimics human reasoning, draft code, summarize papers, and engage in creative dialogue. Yet for many people—even researchers—the inner workings of LLMs remain mysterious. How does a machine take in a string of words and, by crunching vectors and matrices, produce fluent, contextually rich language?

One way to cut through the mystery is to borrow analogies from physics, particularly from quantum mechanics. Among its strangest and most profound phenomena is quantum entanglement. When particles become entangled, they no longer possess separate identities in the way we intuitively imagine. Instead, their states are intertwined such that information about one is inseparable from information about the other.

This essay explores how the concept of entanglement can illuminate the structure and behavior of LLMs. Though the comparison is metaphorical rather than literal, it provides a valuable way of grasping why embeddings, attention, and token prediction feel so uncanny: the system does not manipulate isolated symbols, but rather operates on a tangled web of correlations.

By the end, I’ll argue that “semantic entanglement” is not just a pedagogical metaphor, but a conceptual lens that deepens our understanding of how LLMs model language—and perhaps even how intelligence itself arises from correlation rather than from isolated facts.

—

2. Quantum Entanglement Explained in Plain English

Quantum entanglement is one of those ideas that seems designed to break common sense. In the early 20th century, physicists discovered that particles like electrons and photons could be linked in such a way that their properties became inseparable.

Imagine two coins tossed into the air at the same time. Classical intuition says each coin will land either heads or tails, independent of the other. At most, you might say they were tossed in a way that correlates them slightly—if you flick them with the same force, maybe both are more likely to land heads.

Quantum entanglement is stranger. It is as though the coins share a single fate: if one lands heads, the other is guaranteed tails, and vice versa. What makes this eerie is that the outcome is not determined until one coin is observed. If you check one coin and find it is heads, the other instantly “becomes” tails—even if it is light-years away.

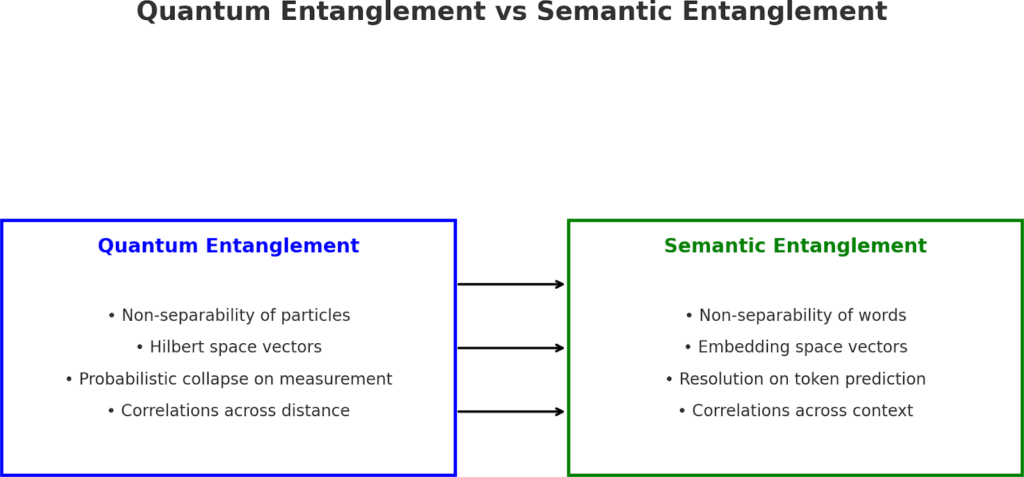
Physicists describe this using Hilbert space, a mathematical setting where a system’s state is a vector that represents a superposition of possibilities. For two entangled particles, the joint state vector cannot be separated into individual vectors. You cannot describe each particle alone; you can only describe them as a coupled system.

This is why entanglement is called non-separability. And it is why Einstein called it “spooky action at a distance.”

—

3. LLMs and Embeddings Explained in Plain English

Now turn to LLMs. At their core, they are pattern-recognition and pattern-generation machines. They process text not as words with dictionary definitions, but as points in a high-dimensional vector space.

Each word or token is assigned an embedding: a vector of hundreds or thousands of numbers. These embeddings are not random. They are positioned so that words used in similar contexts end up close together. “King” and “queen” sit near each other, and the difference between them mirrors the difference between “man” and “woman.”

When the model processes a sentence, it uses an architecture called transformer attention. Attention allows each word to “look at” every other word and adjust its representation based on context. The embeddings shift and update, pulling meaning out of sequences.

The output of all this is a probability distribution over the next token. The model doesn’t “know” in a human sense. It predicts: given this tangled set of embeddings, what is the most likely next word?

Like quantum systems, LLMs operate in high-dimensional vector spaces, use probabilities at their core, and deal with meaning not as isolated pieces but as entangled relationships.

—

4. The Parallels Between Entanglement and Embeddings
   1. Non-separability

Just as entangled particles cannot be described independently, words in an embedding space are not independent. The vector for “apple” contains information about “fruit,” “orchard,” “red,” “sweet,” “tree.” Its meaning only makes sense relative to the geometry of the entire space.

You cannot pluck one embedding out and expect it to carry meaning alone. It is meaningful only because of how it is entangled with thousands of others.

2. Correlation and Constraint

In quantum mechanics, measuring one particle constrains the other’s outcome. In LLMs, activating one concept constrains the field of possible continuations. If the prompt says “quantum,” the next words are constrained toward “physics,” “mechanics,” “entanglement,” and away from “banana.”

3. Collapse vs. Resolution

When a quantum system is measured, its wavefunction collapses into a definite state. When an LLM predicts a token, the probability distribution resolves into a word. Before that, many possible continuations coexist, weighted by likelihood.

4. Global Structure and Local Outcomes

Entanglement means local measurements are tied to global states. In embeddings, a local word choice reflects global semantic structure. A sentence is coherent because every local prediction is conditioned

on the entangled whole.

—

5. Why This Analogy Has Value
   1. Cognitive Aid for Lay Readers

LLMs are notoriously difficult to explain. Saying they are like entangled systems helps people grasp that meaning is relational, not stored in little labeled boxes. It demystifies why models can capture analogy and metaphor so naturally: the geometry itself encodes entangled relationships.

2. Intuition for Developers and Researchers

While the physics is not literally the same, the analogy reminds us that non-separability is fundamental. You cannot fully interpret a neuron’s activation in isolation. You must interpret it as part of the entangled network.

3. Philosophical Implications

Entanglement shows that information is not in objects but in relationships. This resonates with the LLM paradigm: knowledge is not stored as facts, but as statistical correlations. Both cases suggest that reality itself may be correlation-based.

—

6. Limits of the Analogy

No analogy is perfect. Quantum entanglement is physical and experimentally verified. Semantic entanglement is mathematical and statistical. LLMs do not transmit instantaneous correlations across space.

Still, the analogy is productive because it reveals structural similarities: high-dimensional vector spaces, probabilistic resolution, and inseparability of states.

—

7. Deeper Speculative Bridges
   1. Shared Mathematics

Quantum mechanics and LLMs both use linear algebra at scale. States are vectors. Evolution is matrix multiplication. Probabilities come from squared amplitudes (in physics) or softmax scores (in LLMs).

Both systems are probabilistic engines navigating vast state spaces.

2. Non-locality and Long-Range Correlations

Language exhibits long-range entanglement. A word at the start of a paragraph can influence word choice at the end. Transformers are designed to capture these non-local correlations, much as entanglement ties distant particles together.

3. Toward a “Semantic Physics”

One could imagine a physics of meaning, where embeddings evolve under constraints much like wavefunctions. Instead of particles, we have concepts. Instead of observables, we have tokens.

Instead of measurement collapse, we have word generation.

—

8. Implications for AI Research and Philosophy

Thinking of embeddings as entangled opens new avenues:

– Interpretability: Instead of asking what a single neuron “means,” we can study joint entangled subspaces. – Cognitive science: Human thought may itself operate through semantic entanglement—concepts are inseparable from networks of association. – Ontology: Both physics and AI hint that the world is not made of isolated things but of correlations and entangled states.

—

9. Conclusion

Quantum entanglement and LLM embeddings are not the same phenomenon, but they share a profound structural resonance. Both operate in high-dimensional vector spaces. Both encode information in correlations rather than isolated entities. Both produce definite outcomes from probabilistic fields of possibilities.

By drawing this analogy, we gain a clearer picture of why LLMs work as they do. They are not databases of facts but engines of correlation, weaving together entangled representations into coherent streams of language.

And beyond pedagogy, the analogy whispers a deeper truth: intelligence, whether natural or artificial, may not be about storing objects, but about sustaining webs of entanglement—where meaning, like quantum reality, is woven into the fabric of relationships themselves.

Figure: Quantum Entanglement vs Semantic Entanglement